Calculating conductance values
The effective pumping speed required to evacuate a vessel or to carry out a process inside a vacuum system will correspond to the inlet speed of a particular pump (or the pump system) only if the pump is joined directly to the vessel or system. Practically speaking, this is possible only in rare situations. It is almost always necessary to include an intermediate piping system comprising valves, separators, cold traps and the like. All this represents an resistance to flow, the consequence of which is that the effective pumping speed Seff is always less than the pumping speed S of the pump or the pumping system alone. Thus to ensure a certain effective pumping speed at the vacuum vessel it is necessary to select a pump with greater pumping speed. The correlation between S and Seff is indicated by the following basic equation:
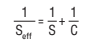
1/S_(eff) = 1/S + 1/C
Here C is the total conductance value for the pipe system, made up of the
individual values for the various components which are connected in series
(valves, baffles, separators, etc.):
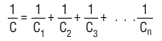
1/C = 1/C_1 + 1/C_2 + 1/C_3 + ... 1/C_n
Equation 1/S_(eff) = 1/S + 1/C tells us that only in the situation where C = ∞ (meaning that the flow resistance is equal to 0) will S = Seff. A number of helpful equations is available to the vacuum technologist for calculating the conductance value C for piping sections. The conductance values for valves, cold traps, separators and vapor barriers will, as a rule, have to be determined empirically.
It should be noted that in general that the conductance in a vacuum component is not a constant value which is independent of prevailing vacuum levels, but rather depends strongly on the nature of the flow (continuum or molecular flow) and thus on pressure. When using conductance indices in vacuum technology calculations, therefore, it is always necessary to pay attention to the fact that only the conductance values applicable to a certain pressure regime may be applied in that regime.
