With the acceptance of the atomic view of the world – accompanied by the necessity to explain reactions in extremely dilute gases (where the continuum theory fails) – the ”kinetic gas theory” was developed. Using this it is possible not only to derive the ideal gas law in another manner but also to calculate many other quantities involved with the kinetics of gases – such as collision rates, mean free path lengths, monolayer formation time, diffusion constants and many other quantities.
Model concepts and basic assumptions:
1. Atoms/molecules are points.
2. Forces are transmitted from one to another only by collision.
3. The collisions are elastic.
4. Molecular disorder (randomness) prevails.
A very much simplified model was developed by Krönig. Located in a cube are N particles, one-sixth of which are moving toward any given surface of the cube. If the edge of the cube is 1 cm long, then it will contain n particles (particle number density); within a unit of time n · c · ∆t/6 molecules will reach each wall where the change of pulse per molecule, due to the change of direction through 180 °, will be equal to 2 · mT · c. The sum of the pulse changes for all the molecules impinging on the wall will result in a force effective on this wall or the pressure acting on the wall, per unit of surface area.
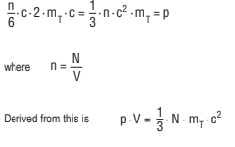
Ideal gas law (derived from the kinetic gas theory)
If one replaces c² with c^(–2) then a comparison of these two “general” gas equations will show:
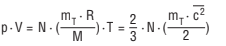
The expression in brackets on the left-hand side is the Boltzmann constant k; that on the right-hand side a measure of the molecules’ mean kinetic energy:
Boltzmann constant
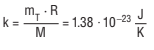
Mean kinetic energy of the molecules
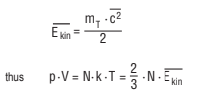
In this form the gas equation provides a gas-kinetic indication of the temperature!
The mass of the molecules is
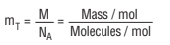
Where N_A is Avogadro's number (previously: Loschmidt number).
Avogadro constant
N_A = 6.022 · 10^(123)mol^(-1)
For 1 mole, m_T/M = 1 and V = Vm = 22.414 (molar volume);
Thus from the ideal gas law at standard conditions (T_n = 273.15 K and p_n = 1013.25 mbar):
p·V = m/(M·R·T)
For the general gas constant:

