The transitional range between viscous flow and molecular flow is known as Knudsen flow. It is prevalent in the medium vacuum range: λ ≈ d. The product of pressure p and pipe diameter d for a particular gas at a certain temperature can serve as a characterizing quantity for the various
types of flow.
Rough vacuum - Viscous flow
λ<(d/100) ⇔ p·d > 6.0·10_(-1) mbar·cm
Medium vacuum - Knudsen flow
(d/100) < λ < (d/2) ⇔ 6·10_(-1) > p·d > 1.3 10_(-2) mbar·cm
High and ultrahigh vacuum - Molecular flow
λ > (d/2) ⇔ p·d < 1.3·10_(-2)mbar ≠ cm
In the viscous flow range the preferred speed direction for all the gas molecules will be identical to the macroscopic direction of flow for the gas. This alignment is compelled by the fact that the gas particles are densely packed and will collide with one another far more often than with the boundary walls of the apparatus. The macroscopic speed of the gas is a “group velocity” and is not identical with the “thermal velocity” of the gas molecules.
In the molecular flow range, on the other hand, impact of the particles with the walls predominates. As a result of reflection (but also of desorption following a certain residence period on the container walls) a gas particle can move in any arbitrary direction in a high vacuum; it is no longer possible to speak of ”flow” in the macroscopic sense.
It would make little sense to attempt to determine the vacuum pressure ranges as a function of the geometric operating situation in each case. The limits for the individual pressure regimes (see Table IX) were selected in such a way that when working with normal-sized laboratory equipment the collisions of the gas particles among each other will predominate in the rough vacuum range whereas in the high and ultrahigh vacuum ranges impact of the gas particles on the container walls will predominate.
In the high and ultrahigh vacuum ranges the properties of the vacuum container wall will be of decisive importance since below 10–3 mbar there will be more gas molecules on the surfaces than in the chamber itself. If one assumes a monomolecular adsorbed layer on the inside wall of an evacuated sphere with 1 l volume, then the ratio of the number of adsorbed particles to the number of free molecules in the space will be as follows:
- at 1 mbar 10–2
- at 10–6 mbar 10+4
- at 10–11 mbar 10+9
For this reason the monolayer formation time τ is used to characterize ultrahigh vacuum and to distinguish this regime from the high vacuum range. The monolayer formation time τ is only a fraction of a second in the high vacuum range while in the ultrahigh vacuum range it extends over a period of minutes or hours. Surfaces free of gases can therefore be achieved (and maintained over longer periods of time) only under ultrahigh vacuum conditions.
Further physical properties change as pressure changes. For example, the thermal conductivity and the internal friction of gases in the medium vacuum range are highly sensitive to pressure. In the rough and high vacuum regimes, in contrast, these two properties are virtually independent
of pressure.
Thus, not only will the pumps needed to achieve these pressures in the various vacuum ranges differ, but also different vacuum gauges will be required. A clear arrangement of pumps and measurement instruments for the individual pressure ranges is shown in Figures 9.16 and 9.16a.
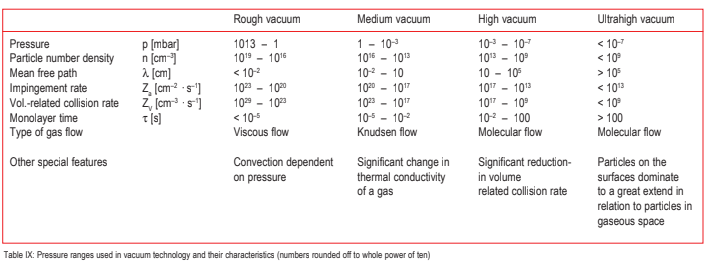
Table IX: Pressure ranges used in vacuum technology and their characteristics (numbers rounded off to whole power of ten)
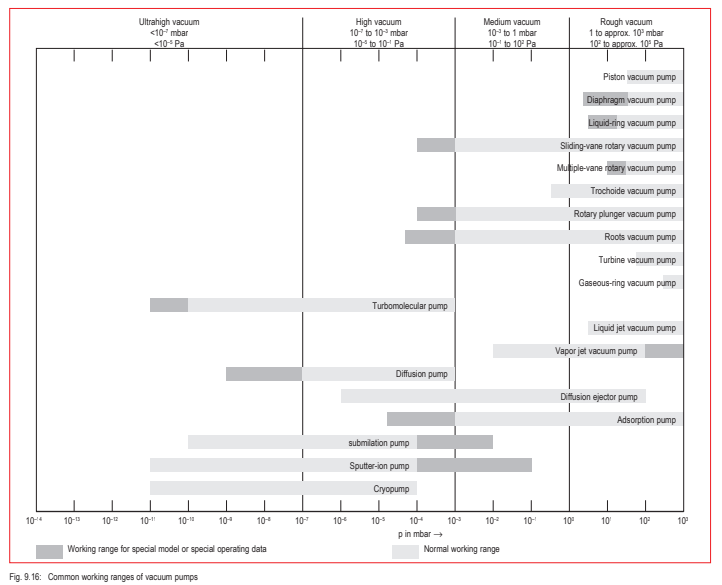
Fig. 9/16: Common working ranges of vacuum pumps
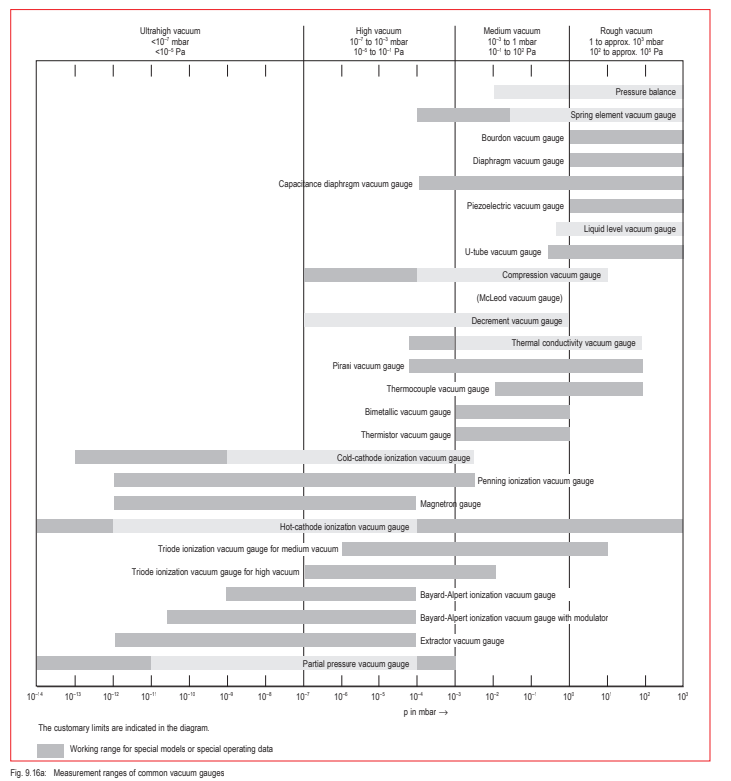
Fig. 9.16a: Measurement ranges of common vacuum gauges
